Asesoría - Matemáticas
LOS NÚMEROS REALES
La Recta numérica
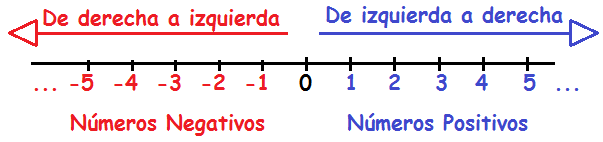

Conjunto ordenado de números que se escribe de forma ordenada sobre una línea horizontal, con marcas a igual distancia, en donde se anotan los números.
Hacia la derecha del cero, se colocan los números positivos y hacia la izquierda del cero, los negativos.
Trazamos la recta L y elegimos un punto sobre ella como origen o cero, tomamos un segmento arbitrario como unidad (U).
Relación de orden
La serie de los números naturales está ordenada de menor a mayor. Así, al ver una serie de números ordenados, podemos saber que los anteriores a un número son menores y los que están ordenados después, son mayores que ese número.
Ejemplo:
1 2 3 4 5 6 7 8 9 10
Sabemos que los números que están antes del 6, son menores a éste (1,2,3,4, y 5) y que los que están colocados después, son mayores, incluso aunque no estén escritos. (Por ejemplo el 25 es mayor que 6)
Números Reales
Los primeros números que aparecieron históricamente fueron los números naturales, utilizados para contar. medir, pérdidas y ganancias y profundidades requerimos el 0 y los números enteros negativos, que junto con los naturales forman el conjunto de los enteros.
En mediciones más precisas se utilizan otro números como los racionales e irracionales que en conjunto forman a los números reales.
NÚMEROS NATURALES._ Son aquellos números que utilizamos para contar.
N = {1,2,3,4,5,6,7,8,9,10,11,…}
NÚMEROS ENTEROS._ Tienen parte decimal nulo.
E = {…-4,-3,-2,-1, 0, 1, 2, 3, 4,5…}
NÚMEROS RACIONALES._ Se pueden expresar como la división de dos enteros.
D = {x/x = a ÷ b; a, b Î E, a ≠ 0}
Algunos elementos de D son:
D = {3/4, -8/5, -6, 0, 1.43, -2.454545…, 2938/34089…}
Entre los números racionales se incluyen:
Todos los enteros positivos y negativos. Ejemplo: 4, -7, 0, 345, etc.
Toda fracción (formada por enteros). Ejemplo: 3/5, 187/456,
Todo número decimal finito. Ejemplo: 3.657, -.2934, 35.39475…
Todo número decimal infinito periódico. Ejemplo: 2.3333…,4.363636…, 0.384384384…, etc.
NUMEROS IRRACIONALES._ No se pueden escribir como la división de dos enteros.
Algunos números irracionales son:
Q = { p, e, √2, √3, √5….}
Contiene a los números con raíces no exactas.
NÚMEROS REALES._ Contiene tanto a los números racionales como a los números irracionales.
Algunos números reales son:
R = {3,-5, 0,3/5,-9/37,p, √7, 1.43,3.656565…, etc.}
+ | con | + | = | + Se suman y se deja el mismo signo | |
- | con | - | = | - Se suman y se dejan el mismo signo | |
+ | con | - | = | Se deja el Signo de mayor valor numérico | |
- | con | + | = | Se deja el signo de mayor valor numérico |
LA DE SIGNOS PARA MULTIPLICAR
| REGLA DE SIGNOS PARA DIVIDIR
|
-5*-3 = 15 -5*3 = -15 | 5*3 = 15 5*-3 = -15 |
15÷5 = 3 -15÷5 = -3 | 15÷-5 = -3 -15÷5 = -3 |
REPASO DE OPERACIONES BÁSICAS
REPASO EXPRESIONES ALGEBRAICAS
SIMPLIFICACIÓN DE TÉRMINOS.- Dos ó más términos semejantes se pueden simplificar en uno solo, operando solo en sus coeficientes.
1) 6x – 10x | 2) -5ab – 7ab + 2.5 | 3) 4.9y + 5.3y – 2.8y |
4) 4a – 2a + 5a | 5) x – 5 – 10x + 5 | 6) 4(z + 5) + 8z |
7) 9y + 3 + 11y + 4 | 8) 3x2 + 2x – 3x2 + 9 | 9) |
1. (2x – 1) (3x + 2) | 2. (5y – 3) ( 8y – 6) | 3. (3x – 9y) (2z – 5w) |
4. (4a + 8) (7a + 9) | 5. (6b + 5) (9b – 10) | 6. (3x – 9y) (2z – 5w) |
7. | 8. (c3 – 2d5) (3c4 + ½ d6) | |
TRINOMIO DE LA FORMA x2 + b x + c = 0
TRINOMIO DE LA FORMA ax2 + b x + c = 0
Introducción Trinomios
Trinomios F.G.
Trinomios F.G. y C.M.
ECUACIONES DE PRIMER GRADO
Repaso
1.- Resolver: x–(34 – x) + 4(x + 1.50) = 10 + 66
2.- Resolver la ecuación (2x – 4) (2x + 4) = 4x (x + 2)
3.- Resolver la ecuación ⅔x – 6 = ⅜ + x
4.- Resolver: 21(.35) + x(.65) = (x + 21) (.40)
5.- Resolver: 10 – 3x ≥ x + 18
6.- Resolver ecuación cuadrática por formula genera: x² - 56x = -768
7.- Resolver: 3x – 6 < 9
8.- Resolver: [1] .80y = x + 1.80
[2] .70y = x + .60
Repaso
1.- Resolver: 4x – (68 – 2x) + 8 (x + 2) = 20 + 132
2.- Resolver la ecuación (4x – 8) (2x + 8) = 4x (2x + 4)
3.- Resolver la ecuación ⅔x – 10 = 1/3 + 4x
4.- Resolver: 46 (.35) + 4x (.65) = (x + 42) (.80)
5.- Resolver: 36 – 6x ≥ 3x – 36
6.- Resolver ecuación cuadrática por formula genera: x² - 56x + 768 = 0
7.- Resolver (Eliminación y Determinantes): [1] 2x –1.60y = 3.60
[2] 2x –1.40y = 1.20
8.- Resolver la siguiente ecuación x² – 30x – 99 = 0
9- Resolver la ecuación: (7x – 2) (5x + 3) = – 54 + 23x + 35x²
10.- Juan compro y pago por 7 camisas $1568, pagando de IVA por cada camisa $30. ¿Cuánto pago por cada camisa?
11.- Resolver: 33 – 12x < – 3x + 99
12.- Resolver (Grafico): [1] 2x - 6y = 18
[2] 4x + 2y = –20
13.- Si se tiene $240 en 33 billetes de a $5 y de a $2 ¿Cuántos billetes son de $2 y cuántos de $5? Resolver por Método de Eliminación.
Resolver TEST Mental
Este test es original de Mensa Internacional. Fue adaptado al español por Mensa España y publicado en la revista ALGO en Enero de 1986. Tiene como máximo 15 minutos para responder las 10 preguntas. No se obtiene mayor puntuación por finalizar antes. Las respuestas erróneas no restan puntos.
Anote en papel sus respuestas.
1. Tomás, Pedro, Jaime, Susana y Julia realizaron el test de Mensa. Julia obtuvo mayor puntuación que Tomás, Jaime puntuó más bajo que Pedro pero más alto que Susana, y Pedro logró menos puntos que Tomás. ¿Quién obtuvo la puntuación más alta?
2. Si fueran dos horas más tarde faltaría para la medianoche la mitad de lo que faltaría si fuera una hora más tarde. ¿Qué hora es ahora?
3. PERA es a MANZANA como PATATA es a:
a) PLÁTANO
b) RÁBANO
c) FRESA
d) MELOCOTÓN
e) LECHUGA
4. Continúe la siguiente serie numérica con el grupo de los números (de entre los propuestos) que mejor la completan:
1 10 3 9 5 8 7 7 9 6 ? ?
a) 11 5
b) 10 5
c) 10 4
d) 11 6
5. ¿Cuál de las siguientes palabras se parece menos a las otras?
a) POEMA
b) NOVELA
c) PINTURA
d) ESTATUA
e) FLOR
6. ¿Qué palabra se obtiene al reordenar las teras SACPRAADAI?
7. ¿Cuál es el número que es la mitad de la cuarta parte de la décima parte de 400?
8. ¿Cuál de las frases que se indican a continuación significa aproximadamente lo mismo que el proverbio: "No cuentes los pollos hasta que salgan del cascarón"?
a) Algunos huevos tienen dos yemas por lo que no se pueden contar realmente huevos y pollos.
b) No se puede caminar por el gallinero para contar los huevos porque esto molestará a las gallinas y no pondrán huevos.
c) No es razonable realmente confiar en algo que no ha ocurrido todavía y que puede que no llegue a suceder.
d) Puesto que los huevos se rompen con tanta facilidad, puede que su recuento de los futuros pollos no resulte muy exacto.
9. Escriba en cada uno de los espacios entre paréntesis una palabra distinta de 3 letras que complete las que figuran a la izquierda y a la derecha de dicho paréntesis. Ejemplo, si colocáramos LAR en ESTE _ _ _ GURA formaríamos ESTELAR y LARGURA.
RIN _ _ _ DE
AC _ _ _ LO
10. ¿Cuál de las cuatro posibles opciones continúa la serie de figuras?
¿Ha finalizado el test?.
RESOLUCION DE PROBLEMAS
En el mundo cotidiano, el primer paso y en ocasiones el más difícil antes de resolver un problema, es el reconocimiento de que ese problema existe
Esto implica que los alumnos no sólo necesitan ayuda para resolver los problemas sino también para reconocerlos. Porque en ocasiones, los problemas se ‘inventan’ de manera tal que formar a los alumnos para que resuelvan problemas que fueron diseñados previamente para ellos, no los prepara, en efecto para realizar una selección por sí mismos de los problemas importantes. En conclusión, a los alumnos habría que enseñarles no solo la forma de resolver problemas sino la habilidad de ser capaces para reconocer los problemas que vale la pena resolver.
Los problemas que aparecerán a continuación serán más o menos originales, por su enunciado, por el procedimiento de resolución, por la solución, etc. etc.
No siempre se darán las soluciones de forma algebraica.
1. LA VIDA DE DIOFANTO. La historia ha conservado pocos rasgos biográficos de Diofanto, notable matemático de la antigüedad. Todo lo que se conoce acerca de él ha sido tomado de la dedicatoria que figura en su sepulcro, inscripción compuesta en forma de ejercicio matemático. Reproducimos esta inscripción:
De lenguaje español a lenguaje algebraico
¡Caminante! Aquí fueron sepultados los restos de Diofanto. Y los números pueden mostrar, ¡oh milagro!, cuán larga fue su vida, x
cuya sexta parte constituyó su infancia. x/6
Había transcurrido además una duodécima parte de su vida, cuando de vello cubriose su barbilla. x/12
Y la séptima parte de su existencia transcurrió en un matrimonio estéril. x/7
Pasó un quinquenio más y le hizo dichoso el nacimiento de su precioso primogénito, 5
que entregó su cuerpo, su hermosa existencia, que duró tan sólo la mitad de la de su padre a la tierra. x/2
Y con profunda pena descendió a la sepultura, habiendo sobrevivido cuatro años al deceso de su hijo. x = x/6 + x/12 + x/7 + 5 + x/2 + 4
2. EL CABALLO Y EL MULO. Un caballo y un mulo caminaban juntos llevando sobre sus lomos pesados sacos. Lamentábase el jamelgo de su enojosa carga, a lo que el mulo le dijo: «¿De qué te quejas? Si yo te tomara un saco, mi carga sería el doble que la tuya. En cambio, si yo te doy un saco, tu carga se igualaría a la mía». ¿Cuántos sacos llevaba el caballo, y cuántos el mulo?
De lenguaje español a lenguaje algebraico
Si yo te tomara un saco x - 1
mi carga y + 1
sería el doble que la tuya. y + 1 = 2 (x - 1)
Y si te doy un saco, y - 1
tu carga x + 1
se igualaría a la mía y - 1 = x + 1
3. LOS CUATRO HERMANOS. Cuatro hermanos tienen 45 duros. Si el dinero del primero se aumenta en 2 duros, el del segundo se reduce en 2 duros, el del tercero se duplica y el del cuarto se reduce a la mitad, todos los hermanos tendrán la misma cantidad de duros. ¿Cuánto dinero tenía cada uno?
De lenguaje español a lenguaje algebraico
Los cuatro hermanos tienen 45 duros. x + y + z + t = 45
Si al dinero del primero se le agregan 2 duros x + 2
al del segundo se restan 2 duros y - 2
el del tercero se duplica 2z
y el del cuarto se divide por, dos, t/2
a todos les quedará la misma cantidad de duros. x+2 = y-2 = 2z = t/2
4. EL REBAÑO MÁS PEQUEÑO. Un granjero que tiene un rebaño de ovejas muy numeroso descubre una gran singularidad con respecto a su número. Si las cuenta de dos en dos, le sobra 1. Lo mismo ocurre cuando las cuenta de 3 en 3, de 4 en 4, etc.... hasta de 10 en 10. ¿Cuál es el rebaño más pequeño que se ajusta a estas condiciones?
5. COMERCIANTES DE VINOS. Dos comerciantes de vinos entraron en París llevando 64 y 20 barriles de vino respectivamente. Como no tenían dinero suficiente para pagar los derechos de aduana, el primero de ellos dio 5 barriles y 40 francos, mientras que el segundo dio 2 barriles, recibiendo 40 francos como cambio. ¿Cuál era el precio de cada barril y su impuesto aduanero?
6. EL PRECIO DE LOS HUEVOS. La señora Rogelia compró un cierto número de huevos, por los que pagó 60 ptas. Al volver a casa se le cayó la cesta rompiéndosele 2 huevos, con lo que el precio le resultó 12 ptas. más caro por docena, con respecto al que pagó inicialmente en el supermercado. ¿Cuántos huevos compró la señora Rogelia?
7. LOS DIEZ ANIMALES. Cincuenta y seis galletas han de servir de comida a diez animales; cada animal es un perro o un gato. Cada perro ha de obtener seis galletas y cada gato, cinco. ¿Cuántos perros y cuántos gatos hay?
8. LOROS Y PERIQUITOS. Cierta tienda de animales vende loros y periquitos; cada loro se vende a dos veces el precio de un periquito. Entró una señora y compró cinco loros y tres pequeños. Si en vez de eso hubiese comprado tres loros y cinco periquitos habría gastado 20 dólares menos. ¿Cuál es el precio de cada pájaro?
9. COCHES Y MOTOS. En un taller fueron reparados 40 vehículos, entre coches y motos. El número total de ruedas de los vehículos reparados fue de 100. ¿Cuántos coches y cuántas motos se repararon?
10. MONDANDO PATATAS. Dos personas mondaron 400 patatas; una de ellas mondaba tres patatas por minuto, la otra dos. La segunda trabajó 25 minutos más que la primera. ¿Cuánto tiempo trabajó cada una?







































Comentarios
Publicar un comentario