ASESORÍA

 

Curso para Admisión

CURSO I

PROPEDÉUTICO DE MATEMÁTICAS

OBJETIVOS: 

La aritmética fundamental de las matemáticas en base a operaciones fundamentales que son: Adición, Sustracción, Multiplicación, División, Potenciación y Radicación.

El programa del curso comprenderá al desarrollo de habilidades matemáticas a través de una serie de actividades que fortalecen y amplían oportunidades del estudiante, promoviendo el desarrollo de procesos en operaciones matemáticas y así para identificar, analizar, generalizar, representar, modelar y resolver problemas de la cotidianos,aplicado la leyes de los signos. 

El curso proveerá de los elementos básicos necesarios para su formación en nivel bachiller, ser individual y social.

Inicio Clase 1

LOS NÚMEROS REALES

La Recta numérica

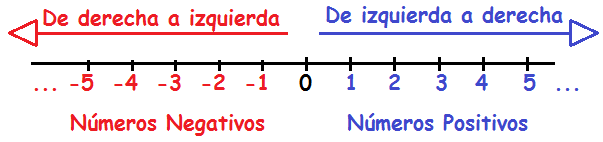
Conjunto ordenado de números que se escribe de forma ordenada sobre una línea horizontal, con marcas a igual distancia, en donde se anotan los números.
Hacia la derecha del cero, se colocan los números positivos y hacia la izquierda del cero, los negativos.

Trazamos la recta L y elegimos un punto sobre ella como origen o cero, tomamos un segmento arbitrario como unidad (U).

Relación de orden

La serie de los números naturales está ordenada de menor a mayor. Así, al ver una serie de números ordenados, podemos saber que los anteriores a un número son menores y los que están ordenados después, son mayores que ese número.

Ejemplo:
1  2  3  4  5  6  7  8  9  10
Sabemos que los números que están antes del 6, son menores a éste (1,2,3,4, y 5) y que los que están colocados después, son mayores, incluso aunque no estén escritos. (Por ejemplo el 25 es mayor que 6)

Números Reales

Los primeros números que aparecieron históricamente fueron los números naturales, utilizados para contar. medir, pérdidas y ganancias y profundidades requerimos el 0 y los números enteros negativos, que junto con los naturales forman el conjunto de los enteros.

 En mediciones más precisas se utilizan otro números como los racionales e  irracionales que en conjunto forman a los números reales.

 

NÚMEROS NATURALES._ Son aquellos números que utilizamos para contar.

N = {1,2,3,4,5,6,7,8,9,10,11,…}

 

NÚMEROS  ENTEROS._ Tienen parte decimal nulo.

E = {…-4,-3,-2,-1, 0, 1, 2, 3, 4,5…}

NÚMEROS RACIONALES._ Se pueden expresar como la división de  dos enteros.

D = {x/x = a ÷ b; a, b Î E, a ≠ 0}

Algunos elementos de D son:

D = {3/4, -8/5, -6, 0, 1.43, -2.454545…, 2938/34089…}

Entre los números racionales se incluyen:

Todos los enteros positivos y negativos. Ejemplo: 4, -7, 0, 345, etc.

Toda fracción (formada por enteros). Ejemplo: 3/5, 187/456,                                             

Todo número decimal finito. Ejemplo: 3.657, -.2934, 35.39475…

Todo número decimal infinito periódico. Ejemplo: 2.3333…,4.363636…, 0.384384384…, etc.

 

NUMEROS IRRACIONALES._ No se pueden escribir como la división de dos enteros.

Algunos números irracionales son:

Q = { p, e, √2, √3, √5….}

Contiene a los números con raíces no exactas.

 

NÚMEROS REALES._ Contiene tanto a los números racionales como a los números irracionales.

Algunos números reales son:

R = {3,-5, 0,3/5,-9/37,p, √7, 1.43,3.656565…, etc.}

REGLA DE SIGNOS PARA SUMA Y RESTA

REGLA DE SIGNOS PARA SUMAR O RESTAR

+	con	+	=	+       Se suman y se deja el mismo signo
-	con	-	=	-        Se suman y se dejan el mismo signo
+	con	-	=	Se deja el Signo  de mayor valor numérico
-	con	+	=	Se deja el signo de mayor valor numérico

SUMA Y RESTA DE REALES

Ejemplos aplicando las reglas de los signos:

1. En suma de números con signos iguales, se suman los números y el resultado lleva el mismo signo. Si  los números tienen signos diferentes, se restan y el resultado lleva el signo del mayor.

Ejemplo:              5 + 8 = 13                    5 + -8 = -3

2. En resta de signos iguales el resultado lleva el signo del mayor. Si se restan signos diferentes, se suman los números y el resultado lleva el signo del mayor.

Ejemplo:              5 - 8 = -3                      5 - (-8) = 13

3. En multiplicación y división de números con signos iguales el resultado es positivo. Si los números son signos opuestos, el resultado es negativo.

Ejemplo:              5 x 8 = 40                     5 x -8 = -40

En esta sección aprenderemos cómo realizar las operaciones entre números reales en una forma sencilla. Aquí te proponemos una forma sencilla para aprender a sumar y restar mediante dos reglas muy fáciles de recordar:

Si se tienen dos números de signos iguales, entonces se suman (entendido como suma en números naturales) y se deja el mismo signo. Ejemplo: 3+5 = 8 esta es una suma común y corriente entre naturales, pero y si fuera -3-5 = -8; observa que igual se obtiene 8 como en la anterior pero esta vez es de signo negativo porque ambos números son negativos y en realidad estamos avanzando hacia la izquierda sobre la recta real.

Si se tienen dos números de signos diferentes, entonces se restan (entendido como resta entre números naturales, el mayor menos el menor) y se deja el signo de la magnitud mayor.

Ejemplo:                         5 – 3 = 2                            -5 + 3 = -2

Mira estos otros ejemplos:

-7+10=3 que es lo mismo que 10 - 7=3                    o   

7-10 = -3 que es lo mismo que –10+7 = -3

a) -4-2-5-10=  -21                                    b) 4+2+5+10= 21

En estos ejercicios largos es buena idea agrupar por signos, así: 

-4+5-10-20+15-7+9 = ?

-4-10-20-7 = -41       5+15+9=29       Y luego restar:      -41+29 = -12

Nótese, que se operó entre los resultados anteriormente obtenidos y se volvió a aplicar la regla. Número de signos diferentes “se restan” y el resultado queda con el signo de la magnitud mayor, en este caso 41.

REGLA DE SIGNOS PARA MULTIPLICACIÓN Y DIVISIÓN

LA DE SIGNOS PARA MULTIPLICAR + * + = + - * - = + + * - = - - * + = -

REGLA DE SIGNOS PARA DIVIDIR + ÷ + = + - ÷ - = + + ÷ - = - - ÷ + = -

MULTIPLICACIÓN Y DIVISIÓN DE NÚMEROS REALES

Ejemplos aplicando las reglas de los signos:

Para estas operaciones es obvio que debes conocer las tablas de multiplicación y división, es decir que signos iguales dan positivo y signos diferentes negativo. 

Ejemplos:

-5*-3 = 15  -5*3 = -15	5*3 = 15  5*-3 = -15
15÷5 = 3 -15÷5 = -3	15÷-5 = -3 -15÷5 = -3

Fin Clase 1

Inicio Clase 2

Fin Clase 2

Inicio Clase 3

Inicio Participación 3

Fin Participación 3

Fin Clase 3

Inicio Clase 4

Fin Clase 4

Inicio Clase 5

Regla de Tres

Inicio Clase 6

PARTE A

1.- Resolver  (3/1) + (1/2 – 1/2) + (4 +3 -2 -3) - (-10) =

2.- Resolver  2 / 9 – 3/2 – ( 2 )  (–1)  – 8 =

3.- Resolver  2 / 3 – 4 / 2 +  5/ 2 + 4 / 3  =

4.- Resolver  a) 80 ÷ __ = 3  R5         

                      b) (20.0)  ( .98) =

5.- Unos 12 kilos de bombones cuestan 5.5 euros, ¿cuánto costarán 100 kilos?

6.- 3/1 + 1/2 – ½  + 4 +3 -2 -3 - (-10)

7.- A Juan le dieron 2/4 de pastel y a Montse 2/5 de pastel. ¿Cuánto reunieron entre los dos?

8.- Un empleado gana diariamente 30 y 2/8 euros y gasta 20 y 1/8 euros ¿Cuánto ahorra diariamente?

9.- Resolver  –1y2/7  +  5y6/9  –  9y5/8 =

10.- Resolver (–4 / 2) (4 / 8) (9 / 3) (–140 / 2) (–110) =

PARTE B

1.- Resolver (2/1) + (3/2 – 1/2) + (6 +3 -2 -3) - (-11) =

2.- Resolver  2/5 – 1/2 –  2   –1  – 8 =

3.- Resolver  (4 / 3) – (2 / 2) – 5/ 2 + 4 / 3   – (–58) =

4.- Resolver  a) 80 ÷ __ = 4  R0         

                      b) (20.3)  ( 0.78) =

5.- Unos 12 kilos de bombones cuestan 5.5 euros, ¿Cuánto costarán 100 kilos?

6.-  3/1 + 1/2 – 4 +3 -2 -3 - (-110) =

7.- A Juan le dieron 1/4 de pastel y a Montse 1/5 de pastel. ¿Cuánto reunieron entre los dos?

8.- Un empleado gana diariamente 38 y 2/8 euros y gasta 12 y 1/8 euros ¿Cuánto ahorra diariamente?

9.- Resolver  –2y2/7  + 1y6/9  – 3y5/8 =

10.- Resolver (–6/ 2) (8 / 8) (12/ 3) (–100 / 2) (–10) =

11.- ¿Qué animal tiene en su nombre las cinco vocales?

Fin Clase 6

INICIO REPASO: SOLUCIÓN PARTE B

FIN REPASO

Inicio Clase 7

EVALUACIÓN

Propedéutico Matemáticas  

Name:                                                                                             Date:                                           

1.- Resolver: (2/1) + (3/2 – 1/3) + (5 +6 -7 -8) - (-15) =

2.- Resolver: 2/5 – 4/3 – 3 –2 – 5 = 

ETC...

Fin 

CURSO II

MATEMÁTICAS I

OBJETIVOS: Reconocerá a los polinomios como expresiones algebraicas y realizará operaciones aplicadas a los polinomios.



INICIO CLASE 1

ALGEBRA

 EXPRESIONES ALGEBRAICAS

SIMPLIFICACIÓN DE TÉRMINOS: Dos ó más términos semejantes se pueden simplificar en uno solo, operando solo en sus coeficientes.

SUMA Y RESTA ALGEBRAICA

Ejemplo 3.3: Simplificar:       a) 4x²y + 3x²y – 2x²y

                                            b) 3x + 2y – x + 5y

                                      c) 3x + 2y – 1

                                            d) 3xy –y² – 4 – xy + 2y² – 2xy

Solución:

a) Todos los términos son semejantes por lo que se simplifican realizando la operación en sus coeficientes: 

(4 + 3 – 2)x²y = 5x²y

b) Los términos semejantes son 3x y –x y por otro lado 2y e 5y, por lo que el resultado es:

3x + 2y – x + 5y = 3x – x + 2y + 5y = 2x + 7y.

c) Ningún término es semejante por lo que el resultado es: 3x + 2y – 1

d) Juntando los términos semejantes queda: 3xy – xy – 2xy – y² + 2y² – 4= 0 + y² – 4 = y² – 4

SIMBOLOS DE AGRUPACIÓN

Los símbolos de agrupación más utilizados son: Paréntesis ( ), Corchetes  [ ], Llaves  { }.

Todos los signos de agrupación son equivalentes, y para eliminarlos se aplican algunos teoremas, en particular las leyes de los signos.

Ejemplo 3.4: Simplificar        3 – (3x – 2) + ( 5 – 2x) – (3x + 3) + (9 – 2x)

Solución:      Suprimiendo los signos de agrupación queda:     3– 3x + 2 + 5 – 2x – 3x – 3 + 9 – 2x =

                                                                                          = -3x – 2x – 3x – 2x + 3 + 2 + 5 – 3 + 9

                                                                                          = -10x +16

Ejemplo 3.5: Simplificar:    x + (y – z) –  [(3x – 2y) + z] + [x – (y – 2z)]

Solución:   Suprimiendo los paréntesis       x + y – z –  [3x – 2y + z] + [x – y + 2z]     

                  Suprimiendo los corchetes     = x + y – z – 3x + 2y – z + x – y + 2z         

                   Simplificando                         = -x + 2y

Actividades a realizar 1.1

Simplificar las expresiones siguientes

1)    6x – 10x	2)    -5ab – 7ab + 2.5	3)     4.9y + 5.3y – 2.8y
4)    4a – 2a + 5a	5)    x – 5 – 10x + 5	6)    4(z + 5) + 8z
7)    9y + 3 + 11y + 4	8)    3x2 + 2x – 3x2 + 9	9)

MULTIPLICACIÓN

Regla de los exponentes para la multiplicación de potencias:   xⁿ  x^m = x^n+m

Ejemplos:     x³ x⁴ = x⁷,      y y³ = y⁴,    z z⁶ z³ = z¹⁰     

Para realizar la multiplicación de monomios, se multiplican los coeficientes numéricos (incluido signo), las literales semejantes (de acuerdo al teorema anterior) y si hay mas literales, solo se agregan al resultado.

Ejemplo 3.6: Multiplicar               7x²y³  por  -8x³y⁵z²

Solución:        (7x²y³) (-8x³y⁵z²) = -56x⁵y⁸z²

Ejemplo 3.7: Multiplicar:           -25a⁵c⁴  por -24a³b⁴c

Solución:        (-25a⁵c⁴) (-24a³b⁴c) =  600a⁸b⁴c⁵

Para multiplicar un monomio por un polinomio, se aplica el postulado distributivo.  

a (b + c) = ab + ac

Ejemplo 3.8: Multiplicar -5x³y por 3x² –  5xy + 4y²

Solución: El monomio -5x³y multiplica a cada término del polinomio

-5x³y (3x² – 5xy + 4y²) = -15x⁵y + 25x⁴y² – 20x³y³

Ejemplo 3.9: Multiplicar  8xy⁴z⁵  por -9x³z² – 5y⁴z + 6

Solución: (8xy⁴z⁵) (-9x³z² – 5y⁴z + 6) = - 72x⁴y⁷z⁷ – 40xy⁸z⁶ + 48xy⁴z⁵

Para multiplicar dos polinomios se aplica la propiedad distributiva reiteradamente, simplificando los términos resultantes.

Actividades a realizar 1.2

      Resolver las siguientes operaciones.

1.      (2x – 1) (3x + 2)	2.      (5y – 3) ( 8y – 6)	3.      (3x – 9y) (2z – 5w)
4.      (4a + 8) (7a + 9)	5.      (6b + 5) (9b – 10)	6.      (3x – 9y) (2z – 5w)
7.	8.      (c3 – 2d5) (3c4 + ½ d6)

FIN CLASE 1

INICIO CLASE 2

División algebraica

TAREA

Repasar ejercicios de División Algebraica

FIN CLASE 2

INICIO CLASE 3

Repaso de División Algebraica

FIN CLASE 3

INICIO CLASE 4

DIVISIÓN ALGEBRAICA

 

Regla de los exponentes para la división de potencias:    aⁿ/a^m = a^{n – m}

 

Ejemplo 3.18:        x⁷/x³ = x⁴,     a⁸/ a⁵ = a³,        y⁶/y = y⁵

 

Para dividir dos monomios, se dividen los coeficientes y se aplica el teorema para las constantes.

 

Ejemplo 3.19:   Dividir   a) 24x⁵y⁷z entre 6x³y⁴        b) 12x³y⁵z² entre 18x³y⁴

 

Solución:  a) 24x⁵y⁷ ÷ 6x3y⁴ = 4x²y³ ,      b) 12x³y⁵z² ÷ 18x³y² = ⅔ y³z²

En el inciso b el coeficiente ⅔ es el resultado de la simplificación de 12/18. La literal y fue eliminada debido a la igualdad de los exponentes.

 

Para dividir dos polinomios se siguen los siguientes pasos:

1. Se ordenan ambos polinomios en orden decreciente respecto al grado de la variable.
2. Se divide el primer término del dividendo entre el primer término del divisor, obteniendo el primer término del cociente.
3. Se suma del dividendo el inverso aditivo del producto del divisor por el primer término del cociente y se obtiene un primer residuo.
4. Se baja el siguiente término del dividendo sumándoselo al residuo anterior.
5. Se divide el primer término de este residuo entre el primer término del divisor, obteniendo el segundo término del cociente.
6. Se procede de manera similar hasta obtener un residuo cero o de grado menor al del divisor.
7. Comprobar el resultado verificando que:

Cociente × Divisor + Residuo = Dividendo

 

Ejemplo 3.20: Calcular  (24y³ – 41y² – 10) ÷ (3y – 4)

 

Solución: Escribimos los polinomios en orden decreciente de acuerdo a los exponentes de y. Escribimos ceros para las potencias de y que no aparecen en el dividendo.

 

Paso 1                          _  8y²_________________        Calcular 24y³ ÷ 3y

                         3y - 4 ) 24y³ – 41y² + 0y - 10  

                                      -24y³ + 32y²                                    Inverso aditivo del producto

         Suma                                 -6y² + 0y               8y² por 3y – 4

 

Paso 2

                                       _8y² – 3y___    _________   Calcular 9y² ÷ 3y

                            3y – 4 ) 24y³ – 41y² + 0y – 10       

                                       -24y³ + 32y²

                                                  -9y² + 0y                        Bajar 0y

                                                    9y² – 12y                     Inverso aditivo del producto

     Suma                                             -12y – 10             3y por 3y – 4

 

Paso 3

                                       _8y² – 3y – 4 _______           Calcular -12y entre 3y

                            3y – 4 ) 24y³ – 41y² + 0y – 10

                                        -24³ + 32y²

                                                  -9y² + 0y

                                                   9y² – 12y

                                                           -12y – 10                Bajar -10

                                                            12y – 16                Inverso aditivo del producto

                  Suma y Residuo                           -26                  -4 por 3y - 4

 

Actividades a resolver 

FIN CLASE 4

INICIO CLASE 5

TRINOMIO DE LA FORMA  x² + b x + c = 0

 TRINOMIO DE LA FORMA  ax² + b x + c = 0

Introducción Trinomios

Trinomios F.G. 

Trinomios F.G. y C.M.

FIN CLASE 5

INICIO CLASE 6

EJEMPLOS DE TRINOMIOS

FIN CLASE 6

INICIO CLASE 7

PARTICIPACIÓN 7: Resolver, los siguientes ejercicios, de fracciones.

FIN CLASE 7

Evaluación Matemáticas 1

FIN 

CURSO III

MATEMÁTICAS II

OBJETIVOS: Reconocerá a los polinomios como expresiones algebraicas y realizará operaciones aplicadas a los polinomios, ecuaciones de primer grado y graficas.

Realizar portada, con porcentajes de evaluación.

INICIO CLASE 1

INTRODUCCIÓN A LAS ECUACIONES

REPASO EXPRESIONES ALGEBRAICAS

SIMPLIFICACIÓN DE TÉRMINOS.-  Dos ó más términos semejantes se pueden simplificar en uno solo, operando solo en sus coeficientes.

Ejemplo 3.3: Simplificar:       a) 4x²y + 3x²y – 2x²y

                                            b) 3x + 2y – x + 5y

                                      c) 3x + 2y – 1

                                            d) 3xy –y² – 4 – xy + 2y² – 2xy

Solución:

a) Todos los términos son semejantes por lo que se simplifican realizando la operación en sus coeficientes: 

(4 + 3 – 2)x²y = 5x²y

b) Los términos semejantes son 3x y –x y por otro lado 2y e 5y, por lo que el resultado es:

3x + 2y – x + 5y = 3x – x + 2y + 5y = 2x + 7y.

c) Ningún término es semejante por lo que el resultado es: 3x + 2y – 1

d) Juntando los términos semejantes queda: 3xy – xy – 2xy – y² + 2y² – 4= 0 + y² – 4 = y² – 4

SIMBOLOS DE AGRUPACIÓN

Los símbolos de agrupación más utilizados son: Paréntesis ( ), Corchetes  [ ], Llaves  { }.

Todos los signos de agrupación son equivalentes, y para eliminarlos se aplican algunos teoremas, en particular las leyes de los signos.

Ejemplo 3.4: Simplificar        3 – (3x – 2) + ( 5 – 2x) – (3x + 3) + (9 – 2x)

Solución:      Suprimiendo los signos de agrupación queda:     3– 3x + 2 + 5 – 2x – 3x – 3 + 9 – 2x =

                                                                                          = -3x – 2x – 3x – 2x + 3 + 2 + 5 – 3 + 9

                                                                                          = -10x +16

Ejemplo 3.5: Simplificar:    x + (y – z) –  [(3x – 2y) + z] + [x – (y – 2z)]

Solución:   Suprimiendo los paréntesis       x + y – z –  [3x – 2y + z] + [x – y + 2z]     

                  Suprimiendo los corchetes     = x + y – z – 3x + 2y – z + x – y + 2z         

                   Simplificando                         = -x + 2y

Actividades a realizar 1.1

Simplificar las expresiones siguientes

1)    6x – 10x	2)    -5ab – 7ab + 2.5	3)     4.9y + 5.3y – 2.8y
4)    4a – 2a + 5a	5)    x – 5 – 10x + 5	6)    4(z + 5) + 8z
7)    9y + 3 + 11y + 4	8)    3x2 + 2x – 3x2 + 9	9)

MULTIPLICACIÓN

Regla de los exponentes para la multiplicación de potencias:   xⁿ  x^m = x^n+m

Ejemplos:     x³ x⁴ = x⁷,      y y³ = y⁴,    z z⁶ z³ = z¹⁰     

Para realizar la multiplicación de monomios, se multiplican los coeficientes numéricos (incluido signo), las literales semejantes (de acuerdo al teorema anterior) y si hay mas literales, solo se agregan al resultado.

Ejemplo 3.6: Multiplicar               7x²y³  por  -8x³y⁵z²

 

Solución:        (7x²y³) (-8x³y⁵z²) = -56x⁵y⁸z²

Ejemplo 3.7: Multiplicar:           -25a⁵c⁴  por -24a³b⁴c

Solución:        (-25a⁵c⁴) (-24a³b⁴c) =  600a⁸b⁴c⁵

Para multiplicar un monomio por un polinomio, se aplica el postulado distributivo.  

a (b + c) = ab + ac

Ejemplo 3.8: Multiplicar -5x³y por 3x² –  5xy + 4y²

Solución: El monomio -5x³y multiplica a cada término del polinomio

-5x³y (3x² – 5xy + 4y²) = -15x⁵y + 25x⁴y² – 20x³y³

Ejemplo 3.9: Multiplicar  8xy⁴z⁵  por -9x³z² – 5y⁴z + 6

Solución: (8xy⁴z⁵) (-9x³z² – 5y⁴z + 6) = - 72x⁴y⁷z⁷ – 40xy⁸z⁶ + 48xy⁴z⁵

Para multiplicar dos polinomios se aplica la propiedad distributiva reiteradamente, simplificando los términos resultantes.

Actividades a realizar 1.2

      Resolver las siguientes operaciones.

1.      (2x – 1) (3x + 2)	2.      (5y – 3) ( 8y – 6)	3.      (3x – 9y) (2z – 5w)
4.      (4a + 8) (7a + 9)	5.      (6b + 5) (9b – 10)	6.      (3x – 9y) (2z – 5w)
7.	8.      (c3 – 2d5) (3c4 + ½ d6)

FIN CLASE 1

INICIO CLASE 2

Repaso Ecuaciones de Primer Grado

Ejemplo 1.

Ejemplo 2.

Ejemplo 3.

Ejemplo 4.

Ejemplo 5.

Ejemplo 6.

Ejemplo 7.

Participación.

TAREA 2

1.-

2.-
Las que no se ven, las dos primeras son:  (-3,3)  (1,-4) 

3.-

FIN CLASE 2

INICIO CLASE 3

ECUACIONES SIMULTÁNEAS - MÉTODO GRÁFICO

PARTICIPACIÓN 3

TAREA 3

FIN CLASE 3

INICIO CLASE 4

FIN CLASE 4

FIN CLASE 5

TRINOMIO DE LA FORMA  x² + b x + c = 0

 TRINOMIO DE LA FORMA  ax² + b x + c = 0

FIN CLASE 5

INICIO CLASE 6

ECUACIONES DE PRIMER GRADO

FIN CLASE 6

INICIO CLASE 7

Participación 7: Repaso-Matemáticas II

1.- Resolver:  x–(34 – x) + 4(x + 1.50) = 10 + 66

 

2.- Resolver la ecuación  (2x – 4) (2x + 4) = 4x (x + 2)

 

3.- Resolver la ecuación  ⅔x – 6 = ⅜ + x

 

4.- Resolver:  21(.35) + x(.65) = (x + 21) (.40) 

 

5.- Resolver:  10 – 3x ≥ x + 18  

 

6.- Resolver ecuación cuadrática por formula genera: x² - 56x = -768

 

7.- Resolver:  3x – 6 < 9   

 

8.- Resolver:      [1]  .80y = x + 1.80                   

                         [2]  .70y = x + .60

 

Tarea 7: Repaso-Matemáticas II

Cuestionario Matemáticas 2

  

1.- Resolver: 4x – (68 – 2x) + 8 (x + 2) = 20 + 132

2.- Resolver la ecuación (4x – 8) (2x + 8) = 4x (2x + 4)

3.- Resolver la ecuación ⅔x – 10 = 1/3 + 4x

4.- Resolver: 46 (.35) + 4x (.65) = (x + 42) (.80)

5.- Resolver: 36 – 6x ≥ 3x – 36

6.- Resolver ecuación cuadrática por formula genera: x² - 56x + 768 = 0


7.- Resolver (Eliminación y Determinantes):     [1]  2x –1.60y = 3.60
                                                                           [2]  2x –1.40y = 1.20


8.- Resolver la siguiente ecuación x² – 30x – 99 = 0

9- Resolver la ecuación: (7x – 2) (5x + 3) = – 54 + 23x + 35x²

10.- Juan compro y pago por 7 camisas $1568, pagando de IVA por cada camisa $30. ¿Cuánto pago por cada camisa?

11.- Resolver: 33 – 12x < – 3x + 99

12.- Resolver (Grafico):   [1]  2x - 6y =  18
                                        [2] 4x + 2y = –20

13.- Si se tiene $240 en 33 billetes de a $5 y de a $2 ¿Cuántos billetes son de $2 y cuántos de $5? Resolver por Método de Eliminación.

 

FIN CLASE 7

FIN CLASE 8

Evaluación Matemáticas II

EXAMEN MATEMÁTICAS II

FIN 

CURSO IV

MATEMÁTICAS III